平均値と中央値の違い・データの読み方とは？

データの特徴を表す数値として代表的なものに平均値と中央値があります。

平均値で記載されているときと中央値で記載されているときと何が違うのでしょうか。

また平均値・中央値と一緒に理解しておきたい標準偏差、標準誤差、四分位範囲、箱ひげ図などについても一緒に見ていきましょう。

これらを理解しておくと、データが何を伝えようとしているのか分かります。

例えば下のようなデータがあったとして、データの読み方を知ると値を見ればどのような背景なのかイメージできるようになりますよ。

• 平均値　50±10
• 中央値　50（40，70）

平均値（mean）

データの総和をデータの個数で割ったものを平均値（mean）といいます。（平均値には何種類かの定義が存在し、これは厳密には算術平均といいます。）

ただ平均だけではその背景は分かりません。40と60の平均も10と90の平均も50ですよね。

そこで背景をより詳細に示すのがばらつきの指標です。

標準偏差（SD）とはデータのばらつきの大きさを表わす指標です。

40と60の場合と10と90の場合では、10と90の場合の方がばらつきは大きくなります。

標準誤差（SE）とはサンプルから得られる推定量そのもののばらつきの大きさ・推定精度を表す指標として利用される数値です。

平均値は基本的に、実験データの代表値として使用されることが多いです。サンプル一つ一つの”ばらつき”を捉えたい場合は標準偏差（SD）を使用します。また、その実験の代表値がどの程度ばらつくのかを知りたい場合は、標準誤差（SE）を利用した方が良いです。

標準誤差（SE）はSD/√nで求められますので、症例数（n）が多くなるほど平均値の見積もり精度である標準誤差（SE）が向上します。精度が向上とは範囲が狭くなるということですので、標準誤差（SE）で求められた値は小さくなります。（SE↓）

説明上、一部計算式も記載しましたが、論文を批判的吟味するうえでは式は覚える必要は全くありませんので安心してください。

読み手側からの推測

平均値と標準偏差（SD）でそのデータの範囲が分かります。

例えば平均値Mean±SDが59.7±4.8の場合、
①60付近のデータが最も多い
②7割弱のデータは55〜65の間にある
③約95％のデータは50〜70の間にある
と推測できます。

±SDは平均値からSD（標準偏差）を足すか引くかです。

つまり±1SDは“平均値＋SD”（59.7＋4.8＝64.5）、“平均値－SD”（59.7－4.8＝54.9）と54.9～64.5の範囲に68％のデータがあるということです。

同様に考えると±2SDは平均値に2回SDを足すか、2回SDを引きます。“平均値＋SD＋SD”（69.3）、“平均値－SD－SD”（50.1）と50.1～69.3の範囲に約95％のデータがあるということです。（より正確には平均値±2SDの中に約95.5%の平均値が含まれるので平均値±1.96SDが95％になります）

論文には平均値±標準偏差までしか書いていませんので、平均値と標準偏差から読み手側が自分でおおまかにでも背景を推測する必要があるということになります。

95%信頼区間（95% Confidence Interval; 95%CI）

95％CIとは「母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に結果で得られた平均値が含まれる」ということです。

逆に言うと「100回中5回はその区間の中に平均値が含まれない」ということになります。

例えば平均値を120として、

1回目の95％CI：100～140

2回目の95％CI：90～150

3回目の95％CI：…

というように平均値120がその範囲内に含まれるのですが、100回のうち5回は95％CIが130～170のように平均値120を含まないということです。

また、95％CIは標準誤差（SE）で計算されるのですが、正規分布の場合の95%CIは、『95%CI=1.96×SE』です。

結果で95％CIが記載されている場合は、標準偏差（SD）のときのように推測は必要ありませんが考え方としては同じです。

中央値（median）

中央値（median）とは、データを大きい順に並べた時の中央の値のことです。データの件数が偶数の場合は、中央の2つの値の平均値を中央値とします。

四分位数はデータを小さい順に並べて、小さいものから順位を付けた時に、

• 25％（全体の1/4の部分）＝25パーセンタイル（＝第一四分位数）
• 50％（全体の2/4＝1/2の部分）＝50パーセンタイル（＝第二四分位数）
• 75％（全体の3/4の部分）＝75パーセンタイル（＝第三四分位数）

に該当する値のことです。

中央値（四分位範囲）が50（40，70）と記載されている場合は、中央値が50で全体の50％のデータが40～70の範囲にあります。

場合によっては中央値（レンジ）で記載されることもあります。

レンジとは観察された最小値と最大値が記載され、その数値がデータの幅を示しています。

中央値（レンジ）が50（40，70）の場合は中央値50は変わりませんが、最小値40最大値70となり、すべてのデータが40～70の範囲にあることになります。

結果をどう示しているかは論文に記載しているはずなので結果を見るときに確認してくださいね。

文章だけだと分かりにくいので箱ひげ図で視覚的に確認していきましょう。

箱ひげ図

中央値の結果を図示するときに箱ひげ図が用いられます。

箱ひげ図の“箱の中の線”が中央値、“箱の下辺”が25％、“箱の上辺”が75％です。

75－25＝50％と箱の中の範囲が全体の50％のデータを表しています。

箱の下にある線が下から10％目を、箱の上にある線が下から90％目（上から10％目）です。箱の上下にある点（・）が範囲外にある外れ値を表しています。

図によっては外れ値を表示せず、最大値・最小値を箱の外の上下の線で表すこともあります。

四分位範囲、箱ひげ図を理解すると中央値のばらつきを推測できますね。

平均値か中央値か

平均値を用いるか、中央値を用いるかはデータの分布が正規分布か非正規分布かどうかで選択されます。

データの分布型（パラメトリック・ノンパラメトリック）

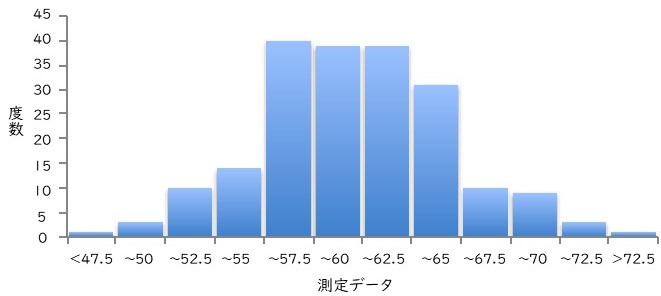
正規分布とはパラメトリックともいい、『グラフにしたときに数値の大半が中央に集中し、平均値を中心に両側均等に分布するデータ』のことを言います。言い換えると左右対称の釣り鐘型となるデータです。

非正規分布とはノンパラメトリックともいい、グラフにしたときに正規ではない分布のデータのことを言います。つまり『グラフにしたときに数値の大半が中央に集中せず、平均値を中心に両側均等に分布しないデータ』となります。片側に尾を引いたような分布で左右非対称のデータです。

さて、平均値、中央値は分布型で決まると言いました。

正規分布のときに平均値を、非正規分布のときに中央値を用います。

平均値も中央値もそのデータの全体像を表すため（読み手側からだと把握するため）に用いるものです。

例えば、正規分布（1，2，3，4，5）、非正規分布（2，2，2，4，5）というデータがあった場合、両方とも合計15で平均値は3になりますが、中央値は正規分布では3ですが非正規分布では2となります。（上の図のようなイメージのグラフを思い浮かべてください。）

中央値と平均値は正規分布のときは一致しますが、それ以外は中央値と平均値は一致しません。

非正規分布のときに平均値を使用しても全体像が把握できないため適さないということがなんとなく分かっていただけたのではないでしょうか。

まとめ